この記事は、物理学アドベントカレンダー202515日目の記事です。

今年2025年のノーベル物理学賞は「電気回路における巨視的量子トンネル効果とエネルギー量子化の発見」によりJohn Clarke（UC Berkeley）、Michel H. Devoret（Yale, UC Santa Barbara）、John M. Martinis (UC Santa Barbara)の3氏が受賞することになりました。

今学期、私はたまたまDevoretとMartinisが所属するUC Santa Barbaraに滞在していたので、ノーベル賞発表直後はちょっとしたお祭り気分を味わうことができました。いい機会だと思い、ノーベル賞の対象となった超伝導量子回路の勉強を少ししたので、その内容をこちらに書いてみたいと思います。

本記事では学部レベルの量子力学をもとに、超伝導量子回路の基礎的な部分をまとめます。特に、超伝導量子回路がどうして量子的にふるまうのかについて、私の専門でもある固体物理の観点から説明してみたいと思います。

基本的には学部生にもわかることを目指して書いています。数式をたくさん使うというよりは、なるべく直感的な例をたくさん出して解説したつもりです。

前提知識としては、学部で習う程度の量子力学の基礎を仮定します。一部バンド理論の言葉が出てきますが、知らなくても内容を理解するのにそれほど支障はないと思います。超伝導については、抵抗ゼロであるということと、電子がペアを組んだクーパー対が形成されているということを用います。超伝導そのものについては解説しません。

本記事の内容は基本的にSteven M. Girvinが書いた講義ノートをもとにしています。固体物理を専門にしている私にとっては、同じく固体物理の専門家でもあるGirvinが書いたこの解説は非常にわかりやすく感じました。この解説を通じて固体物理としての超伝導もより深く理解できたような気がします。興味のある方はぜひGirvinの解説を直接読んでみてください。

内容には自分なりに万全を期したつもりですが、超伝導回路は専門ではないこともあり、誤りがあるかもしれません。もし何か誤りを発見したらお知らせいただけると大変ありがたいです。

1. マクロな量子系としての超伝導量子回路

量子力学はミクロな系、例えば電子や原子を支配する物理法則であり、不確定性関係やエネルギーの量子化といった、古典力学にはない特徴を数多く持っています。しかし、電子や原子が寄り集まって、例えば机や鉛筆といった日常的なサイズのモノになると、こうした量子力学特有の振る舞いは通常見えなくなってしまいます。

今年のノーベル賞の対象となった実験は、膨大な数の原子でできたマクロな系であっても、特定の条件下では量子的な振る舞いがみられることを示しました。より具体的には、超伝導量子回路と呼ばれる、超伝導体でできた散逸のない電気回路においても、量子トンネル効果とエネルギー量子化がみられることを実験的に明らかにしました。

本記事では、どうして超伝導量子回路ではマクロな系であるにもかかわらずこれらの量子的振る舞いが観測されたのか、特に、エネルギー量子化を観測するための実験的な必要条件について、私なりに説明してみたいと思います。

ある系において量子効果を実験で観測するには、少なくとも二つ条件を満たす必要があります。一つは、その系の散逸が小さいことです。散逸が大きすぎると、エネルギー準位が「ぼやけて」しまい、量子化を観測することができません。もう一つの条件は、低エネルギー状態が多すぎないことです。低エネルギー状態が多すぎると、やはりエネルギー準位の量子化が非常に観測しづらくなるほか、量子状態を制御するのも難しくなります。以下では、これらの二つの条件がどうして必要なのか、また、超伝導回路ではこれらの（特に二つ目の）条件をどのように満たしているのかについて考えます。

2. 散逸とエネルギー準位の「ぼやけ」

エネルギー量子化を観測するには、散逸が十分少ない系を考える必要があります。一般に散逸があると、エネルギー準位は「ぼやけて」しまい、個々のエネルギー準位をはっきり見ることはできません。このことを見るために、以下のような簡単なケースを考えてみましょう。一次元の無限に深い井戸型ポテンシャルに閉じ込められた量子力学的な粒子が、散逸の中でどう振る舞うかを考えます。ハミルトニアンは運動量を$p$、質量を$m$として$H=p^2/(2m)$で与えられ、波動関数は境界条件$\psi(x=0)=\psi(x=L)=0$に従います。この時エネルギー準位は以下のように量子化します。

ここで$n$は整数です。

さて、この系においてエネルギー準位を実験的に観測することを考えます。まずは散逸がない場合を考えましょう。通常の固体物理などの実験では、例えば光を当てた時の共鳴周波数を見ることでエネルギー準位を決めますが、ここではこの状況を簡単化して、次のように考えてみましょう。何らかの方法で、時刻$t=0$に系の基底状態$\psi_0(x)=\sqrt{2/L}\sin(k_0x)$と第一励起状態$\psi_{1}(x)=\sqrt{2/L}\sin(k_1 x)$の重ね合わせを作れたとします。系の状態は例えば

のようになります。ここで$\alpha$は$0\le\alpha\le1$を満たし、$\alpha^2$が$\psi_1$への励起された確率を表します。

系に散逸がない場合にはこの状態の時間発展は次で与えられます。

この状態をつかうと、基底状態と第一励起状態のエネルギー差を実験的に観測することができます。例えば、各時刻$t$における粒子の位置を測定すると。

ここで$c_1=-32L \sqrt{1-\alpha^2}/(9\pi^2)$は計算するとわかる適当な定数です。重要なのは$x$の時間依存性を決める周波数$\Omega$で、これは重ね合わせに使われた状態のエネルギー差で与えられます。

したがって、散逸がない場合には、$\langle x\rangle(t)$の振動の周波数を見てやれば、エネルギー準位（の差）を実験的に測定できることになります。$\langle x \rangle(t)$をフーリエ変換すれば、デルタ関数的なピークが$\omega=\pm\Omega$に立つのが見えるはずです。

次に散逸がある場合について考えてみましょう。散逸があるということは、励起を含む状態$\psi(x, t)$は、時間がたつとどこかでエネルギーを放出して基底状態に戻ってしまうということです。いつ、どのようにエネルギーを出して基底状態に戻るのかは散逸のメカニズムなど実験の詳細によるでしょうが、ここではこの様子を励起の確率振幅$\alpha$に次のように時間依存性を入れることでモデル化してみましょう。

（今回は指数関数的に減衰するとしましたが、エネルギー準位がぼやけることを見るだけなら適当な減衰関数ならなんでもよいです。）$\gamma$は散逸の強さに対応していて、励起状態がおおよそ時間$t=1/\gamma$くらいで基底状態に戻ってしまう様子をモデル化しています。 この置き換えをすると、位置の期待値の振る舞いは、$\alpha^2\ll 1$の場合には以下のようにふるまうことが容易にわかります：

この式は、励起した状態が$1/\gamma$程度の時間で基底状態に戻ってしまうので、位置の振動もやはり$1/\gamma$程度の時間で止まってしまうことを表しています。極端な話、もし$\gamma$が$\Omega$よりも大きければ、位置が一回振動するよりも早く振動が止まってしまうので、振動の周波数を観測することも事実上不可能になるでしょう。

このことはフーリエ変換をすることによってもわかります。$\langle x \rangle(t)$のフーリエ変換は$e^{-\gamma t}$の因子のためにデルタ関数的なピークではなくなり、$\gamma$程度の広がりを持つことになります。$\gamma$がエネルギー準位間の差に比べてあまりに大きいと、エネルギー準位を示すピークはぼやけて実験的に観測できなくなってしまいます。

以下の図は、散逸なし（undamped）、あり（damped）のそれぞれの場合について、時間領域と周波数領域での振動を示したものです。散逸がある場合には振動の振幅がだんだん減衰していき、対応して周波数領域ではピークがぼやけているのがわかります。

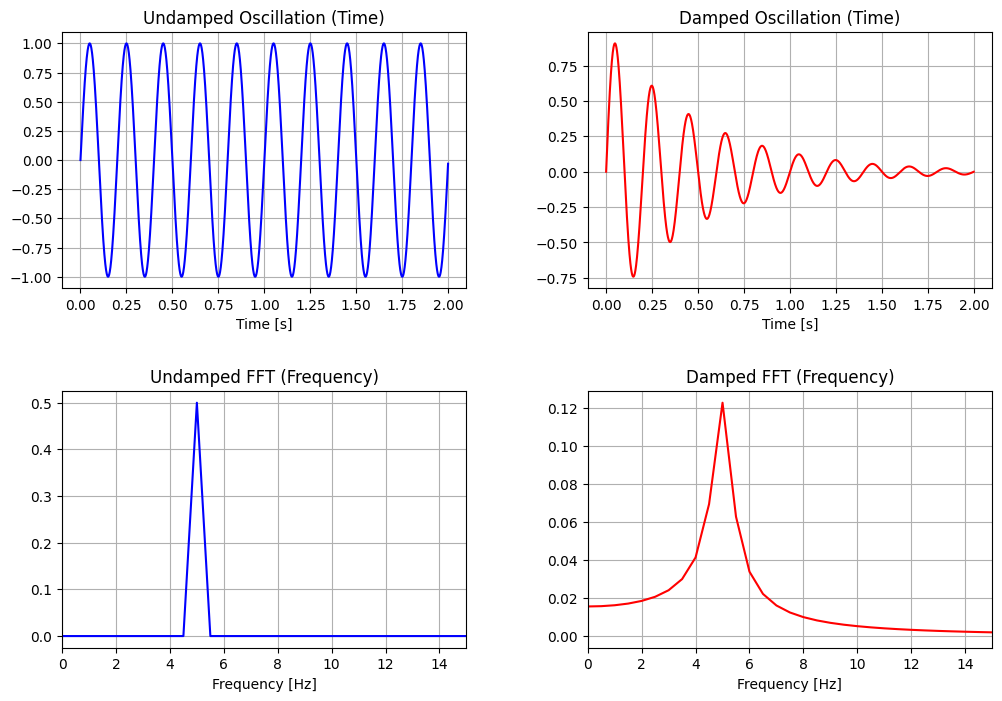
したがって、エネルギー準位を測定し量子化を見るためには、散逸は十分に小さい必要があることがわかりました。通常の金属では有限の抵抗によって散逸が起こるため、エネルギー準位の量子化の直接観測は期待できませんが、超伝導体ではゼロ抵抗で散逸がないためエネルギー量子化を見るのによい系になると期待できます。

3. 低エネルギー状態の有効モデルとしての電気回路

量子効果の観測に必要なもう一つの条件は、低エネルギー状態が多すぎないことです。ここでいう低エネルギー状態とは、実験的に扱いが容易なエネルギー領域（低エネルギー領域）にある状態のことを指します。電気回路の場合、ほとんどの実験は1-10 GHz程度の周波数およびそれに対応するエネルギー（1-10 $\mu$eV程度）で行われます。この程度のエネルギーを持つ状態が低エネルギー状態に相当します。

低エネルギー状態が多いと、たくさんのエネルギー準位が一部のエネルギー領域に密集することになるので、ほんのわずかな散逸による準位の「ぼやけ」でもエネルギー量子化が見えなくなり、実験による観測が難しくなります。また、状態が多すぎると、量子状態の制御も難しくなることも想像に難くないでしょう。もちろん、低エネルギー状態が全くないというのも困ります。低エネルギー状態が程よい数存在するような系が、量子効果の観測に必要になります。

どのような系が適度な数の低エネルギー状態を持つでしょうか。例えば、通常の金属では大量の低エネルギー状態が存在します。バンド理論の言葉で言うと、フェルミ面付近の電子状態はすべて無限小のエネルギーを持つ励起に対応するので、低エネルギー状態の数はフェルミ面の面積に比例します。マクロな金属を考えた場合には、これでは状態の数があまりにも多すぎます。金属において超伝導回路のような量子効果を実験で見るのが難しいのは、もちろん散逸の問題もありますが、このように低エネルギー状態が多すぎることも理由の一つでしょう。

絶縁体ではどうでしょうか。例えばバンド絶縁体だと、バンドギャップ以下の低エネルギー状態は存在しません。¹ バンドギャップは通常1 eV（~1000 THz）くらい、小さくても数meV（~1 THz）程度のスケールなので、電気回路の1-10 GHz程度のエネルギー領域には何も励起状態が存在しないことになります。これはこれで量子効果の観測には困ってしまいます。

超伝導体だとどうでしょう。まず、超伝導体では、金属のような大量の低エネルギー励起はなくなります。これは、超伝導状態では電子同士に引力が働くために、クーパー対と呼ばれるペアを組んだ状態が最も安定になっているからです。金属のフェルミ面の各点に対応する低エネルギー励起、つまり、電子一つが励起されているような状態を作るにはクーパー対を壊す必要がありますが、クーパー対を壊すのに必要なエネルギーは通常数百$\mu$eV~数meVなので、電気回路でアクセスできるようなエネルギー領域ではなくなります。²

金属での低エネルギー励起がすべてなくなっているのであれば、ちょうどいい低エネルギー状態は超伝導状態にはまったくないのでしょうか。実はそういうわけでもありません。金属・超伝導体においては、もう一つプラズモンと呼ばれる集団励起があります。プラズモンとは、大量の電子がまとまって振動するような励起のことを指します。ここまで触れてきたフェルミ面付近の励起は、あくまで系の中の一つの電子を少しエネルギーの高い状態に持っていくことでできる励起でしたが、プラズモンはたくさんの電子を一斉に動かすことでできる励起です。

最も簡単なプラズモンのモデルは次のように考えることができます。一様な正の背景電荷の上で電子が一様に分布しているようなモデルを考えましょう。電子密度を$n$とし、背景電荷と合わせて系全体は電荷中性とします。基底状態は電子が正の背景電荷上を一様に分布している状態としましょう。この時、上図のように電子全体が一様にずれるような励起を考えましょう。図のように電子がずれると、左側に正の背景電荷が露出し、一方右側には背景電荷に打ち消されない負の電荷が現れます。その結果、左から右へ電場が発生し、ずれた電子は元の位置に引き戻される復元力を感じます。この復元力によって生じる振動モードが、プラズモンに他なりません。

プラズモン励起の振動数を考えるために、電子の重心運動がどのように記述できるか考えてみましょう。 電子の重心が基底状態から$X$だけずれたとき、両端に現れる電荷の量は$Q=nXS$と書けます。ここで$S$は上図の画面奥行き方向の表面積です。このときこの電荷によって生じる電場$E$は、$X$が系全体の大きさに比べて十分小さいとすれば、

ここで$\epsilon_0$は誘電率です。³ したがって、電子の重心にかかる復元力は重心変位$X$に比例することがわかります。運動方程式は次のように書けます。

ここで$N$は電子の総数、$M=Nm$は電子の総質量、$e(<0)$は電子の電荷です。これはすなわち、電子の重心運動のハミルトニアンとして、次のような調和振動子を考えるのと等価です：

ここで$P$は重心$X$に共役な運動量で、$\omega_p=\sqrt{ne^2/(m\epsilon_0)}$は対応するプラズモンの振動数です。$\omega_p$はプラズマ周波数と呼ばれています。

今回は非常に単純化してあたかも電荷が物質の端にしか現れないような図を書いていますが、実際の物質中では、電子の粗密波の振動がプラズモン励起に対応します。電子の粗密波ができると電荷分布が生じ、それによって電場が発生して粗密波を一様に戻すような復元力が働くので、結果的に電子の粗密波が振動します。これがより一般的なプラズモン励起です。粗密波の波長によって、プラズモン励起のエネルギーも変わるため、プラズモン励起の分散関係を考えることもできます。一般的な粗密波でも、プラズモンの波長$\lambda$が電子の波長$\lambda_F$に比べて十分大きければ、上記と同じプラズマ振動数を与えることが示せます。

通常の金属中では、プラズマ振動数は非常に大きく、おおよそ10 eV程度のオーダーです。これは電気回路の振動数よりもはるかに大きいため、通常無視できます。したがって、こうしたプラズモン励起も、ほとんどは無視できます。

しかし、プラズモンの波長が系の大きさと同程度になると、実は一般には上記の計算はあまり信用なりません。例えば上に示したプラズモンの図の代わりに、物質の形を長方形からコの字形に変えたらどうなるでしょうか。もし電子がずれて下図のように電荷が現れた場合、生じた電場によって電子にかかる力は上記の計算と同じにはならないことは容易に想像できます。このように、プラズモンの波長が系の大きさ程度の場合には、プラズモンの振動数は、系の形に依存します。逆にいうと、系の形をうまく制御してやれば、波長が非常に長いプラズモンの振動数を大幅に変えることができます。

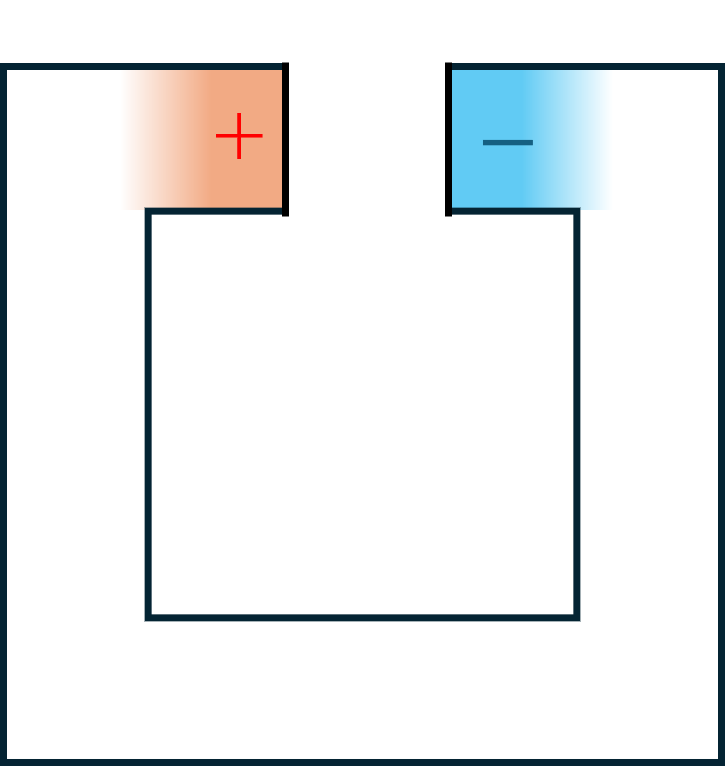
このような系の形によるプラズモンの効果は、実は高校で習うコンデンサの効果に他なりません。実際上のコの字状の金属の図は、電荷がたまる部分をコンデンサ、それ以外の部分をコンデンサをつなぐ導線だと思えば、以下に示すコンデンサを短絡したような回路と思うことができます。対応して、波長の長いプラズモンに働く復元力、ないし対応するポテンシャルは、系の形によって決まる電気容量$C$を使って現象論的にモデル化することができます。系の端にたまる電荷を$Q$とすれば、対応するポテンシャルは

と書けます。

以上では電荷密度の変化によってできる電場（復元力）、および対応するポテンシャルが系の形に依存し、それは電気容量によってモデル化できることを見てきました。さらによく考えると、電荷が動いている（電流が流れている）ときのエネルギーも、波長が長い時には系に依存することが想像できます。例えば、金属によって作られた導線がコイルを巻いていれば、電流が流れたときにコイル中に磁場が誘導されるため、同じ電流を流すのにも磁場エネルギーだけ余分なエネルギーが必要になります。このように、プラズモンの運動エネルギーも系の形状に依存することがわかります。この効果は、対応するインダクタンスを導入することでモデル化できます。プラズモンの運動エネルギーは、インダクタンス$L$、電流$I$を用いて、

と書けます。

したがって、系の長波長のプラズモンの実効的なモデルは、運動エネルギー$K=LI^2/2$、ポテンシャルエネルギー$V=Q^2/2C$とすれば、対応するラグランジアンを$\mathcal{L}=K-V$と定めることで得られます。適当に$L$と$C$を設計してやれば、実験的にアクセス可能な周波数領域に長波長のプラズモン励起を作ることができます。

以上の議論は、金属だけでなく超伝導体でも同じように成立します。特に超伝導体の場合には、金属と違って散逸がないので、前節で議論したようにプラズモン励起による振動が長く生き残ります。またすでに述べたように、その他の励起ははるかに大きなエネルギーを持つため、このような長波長のプラズモンが低エネルギー領域に隔離された励起になります。このプラズモン励起も原理的には量子論に従っているはずですから、プラズモン励起のエネルギー量子化といった量子現象が超伝導量子回路上で観測できると期待できます。

終わりに

ここまで、超伝導量子回路がなぜ量子的に振る舞うのかについて、固体物理的な観点から考えてみました。超伝導量子回路では散逸がないこと、そして低エネルギー状態を系の形状を用いて制御できることから、マクロな系であるにもかかわらず量子現象の観測が期待できることを議論しました。 実際の実験では、これらの条件に加えて、温度を十分に下げ熱揺らぎを抑制し、さらに量子的な振る舞いを観測するための測定装置が超伝導量子回路を乱しすぎないような実験を組み立てる必要があります。Clarke、Devoret、Martinisはこうした実験を1980年代に行った先駆的な研究で、今回ノーベル賞を受賞したということになります。

私はトポロジカル物質などの理論が専門で、普段はバンド理論のようなことばかり考えているので、電気回路の観点から物質の励起について考えるのは新鮮で面白かったです。今回参考にしたGirvinのcircuit QEDの講義ノートは大変すばらしいので、興味を持った方はぜひ読んでみてください。